双向宽度优先搜索

BFS（宽度优先搜索）是我们最先接触的几个算法之一，和DFS（深度优先搜索）一起，成为初学者必学的两大搜索算法。使用队列这种先进先出的数据结构，在遍历图、树等方面有着巨大的作用，同时由BFS优化而来的SPFA最短路径算法、Dijkstra最短路算法等，也是非常经典的算法。

今天我要介绍的是一种不一样的BFS，以 P1379 八数码难题 - 洛谷 为例，介绍双向BFS。

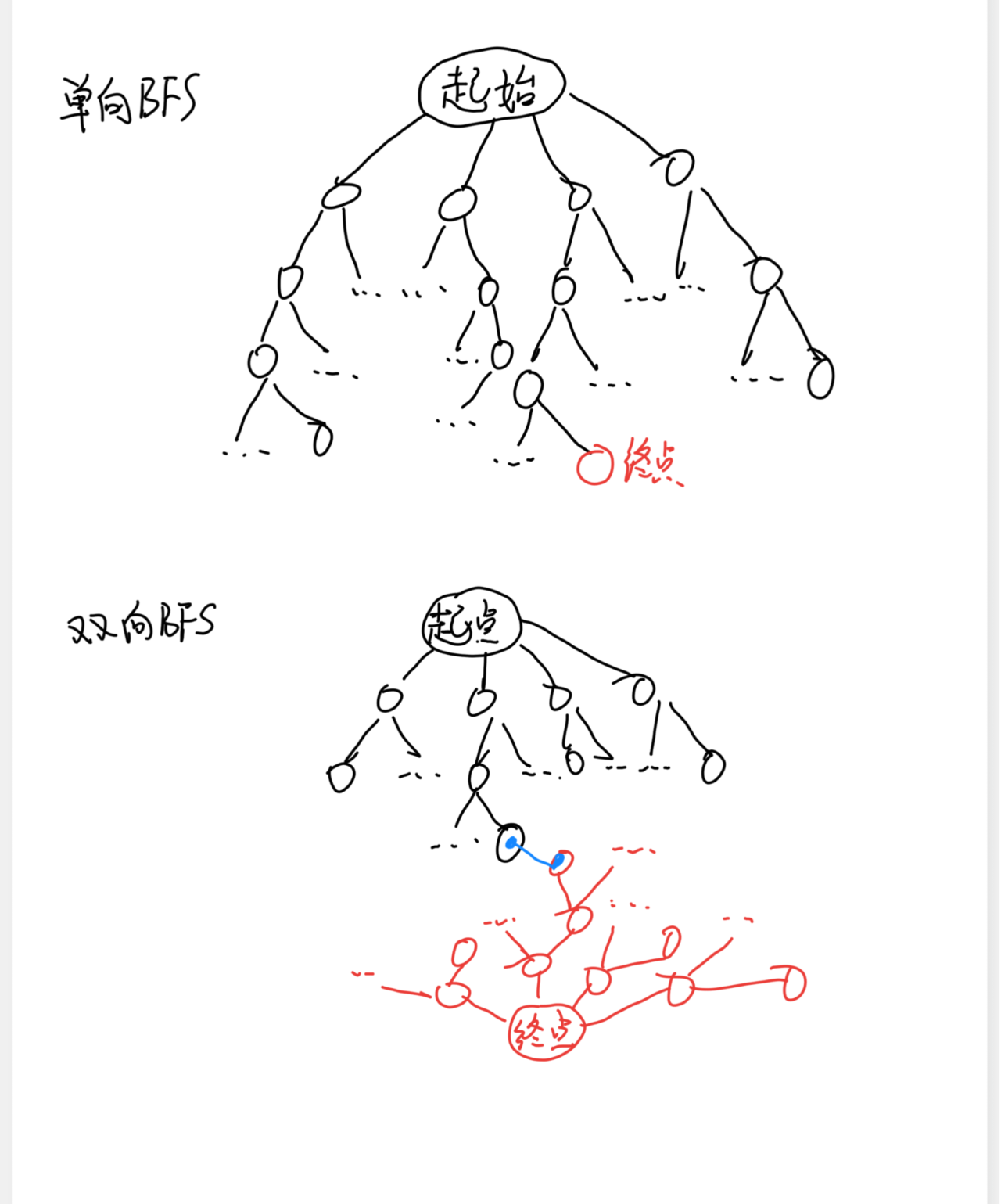
对于一种起始状态和终末状态确定的搜索，很容易就能想到我们可以同时从头和尾开始搜索，直到搜索树相交时，我们就可以找到路径，这就是双向BFS。

以下这个图简单的介绍了双向BFS的原理：

8710efff19adca6a997e7d9de44fa81e_720

题目描述

在 3×33\times 3 的棋盘上，摆有八个棋子，每个棋子上标有 11 至 88 的某一数字。棋盘中留有一个空格，空格用 00 来表示。空格周围的棋子可以移到空格中。要求解的问题是：给出一种初始布局（初始状态）和目标布局（为了使题目简单,设目标状态为 123804765123804765），找到一种最少步骤的移动方法，实现从初始布局到目标布局的转变。

输入格式

输入初始状态，一行九个数字，空格用 00 表示。

输出格式

只有一行，该行只有一个数字，表示从初始状态到目标状态需要的最少移动次数。保证测试数据中无特殊无法到达目标状态数据。

样例 #1

样例输入 #1

1
283104765

样例输出 #1

1
4

提示

样例解释

图中标有 00 的是空格。绿色格子是空格所在位置，橙色格子是下一步可以移动到空格的位置。如图所示，用四步可以达到目标状态。

并且可以证明，不存在更优的策略。

一、思路

首先，我们观察到题目的输入格式，给我们提供了一个很好的暗示，我们可以将状态压缩成一个数进行存储，这样我们就可以做到记录下访问的节点，从而做到两棵搜索树的相交。

首先我们需要两个函数来实现地图和状态的相互转换：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int mmap[5][5];        // 存储地图
int startx, starty; // 存储初始位置
void toMap(int num) // 实现将一个数字转化为地图
{
    for (int i = 3; i >= 1; i--)
        for (int j = 3; j >= 1; j--)
        {
            mmap[i][j] = num % 10;
            num /= 10;
            if (mmap[i][j] == 0) // 在转化地图过程中，如果发现“0”，那么记录初始位置
            {
                startx = i;
                starty = j;
            }
        }
}
int toNum() // 实现将地图转化为数字
{
    int num = 0;
    for (int i = 1; i <= 3; i++)
    {
        for (int j = 1; j <= 3; j++)
        {
            num = num * 10 + mmap[i][j];
        }
    }
    return num;
}

其次，我们需要记录图搜索的过程。一个容器记录搜索树的搜索记录，记录该节点是顺序访问还是逆序访问。一个容器记录走到该节点的路程，可以使用STL中的map容器，节省空间。

1
2
3
4
5
6
7
8
9
10
map<int,int> vis,ans;
// vis容器存储访问情况，1表示顺序访问，2表示逆序访问
// ans容器存储节点的搜索路径长度
queue<int> q;   //搜索的队列
int startx,starty;
int mmap[5][5];
int endmap=123804765;  //逆序搜索起点（目标状态）
int dx[4]={0,1,0,-1};
int dy[4]={1,0,-1,0};
//四个方向

最后是核心的双向bfs过程请详细看以下代码

二、代码

核心的双向bfs过程请详细看以下代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <bits/stdc++.h>
using namespace std;
int t;
map<int,int> vis,ans;
// vis容器存储访问情况，1表示顺序访问，2表示逆序访问
// ans容器存储节点的搜索路径长度
queue<int> q;   //搜索的队列
int startx,starty;//记录地图中”0”的位置
int mmap[5][5];//存储地图
int endmap=123804765;  //逆序搜索起点（目标状态）
int dx[4]={0,1,0,-1};
int dy[4]={1,0,-1,0};
//四个方向
void ToMap(int num){  //数字转化为地图
    for (int i=3;i>=1;i--){  //注意转化地图的时候需要反向读入地图
        for (int j=3;j>=1;j--){
            mmap[i][j]=num%10;
            num/=10;
            if (mmap[i][j]==0){  //记录地图中“0”的位置
                startx=i;
                starty=j;
            }
        }
    }
}
int ToNum(){  //地图转化为数字
    int num=0;
    for (int i=1;i<=3;i++)
        for (int j=1;j<=3;j++)
            num=num*10+mmap[i][j];
    return num;
}
int main(){
    cin>>t;
    if (t==endmap){
        cout<<"0"<<endl;
        return 0;
    }

    q.push(t);
    q.push(endmap);
    //将起始状态和目标状态都入队
    ans[t]=0;
    ans[endmap]=1;
    //起始状态步数为0，目标状态步数至少是1
    vis[t]=1;
    vis[endmap]=2;
    //起始状态是顺序访问，目标状态是逆序访问
    while(!q.empty()){
        int current=q.front();//取出队列头
        q.pop();
        ToMap(current);
        for (int i=0;i<4;i++){//四个方向挨个搜索
            int x=startx+dx[i];
            int y=starty+dy[i];
            swap(mmap[startx][starty],mmap[x][y]);
            int temp=ToNum();
            if (vis[temp]==vis[current]){//如果同样顺序已经访问过，则跳过
                swap(mmap[startx][starty],mmap[x][y]);
            }
            else if (vis[temp]+vis[current]==3){//逆序搜索与顺序搜索已经相遇
                cout<<ans[temp]+ans[current]<<endl;//直接输出最短路径
                return 0;
            }
            else {
                vis[temp]=vis[current];
                ans[temp]=ans[current]+1;
                q.push(temp);
                swap(mmap[startx][starty],mmap[x][y]);//回溯
            }
            
        }
    }
    return 0;
}